Hi,
I've found 2 bugs in show ep asym. This doesn't change results from
chris and tong last night. I add the false asymmetries. Also expanded
show_ep_asym.C and just took out charge from lrn.C all together (see
init.C). Inserted a protection into charge.C for runs with no epics (no
change however, all good runs!)
_ For the average asymm (shown last night) there was an inconsistent
normalization
_ For the false asymmetries: they were a sum of two asymmetries, which is
just wrong (numerator and denominator have to be both right)
New false asymmetry results attached. Small but not entirely zero.
Definitions: (for everybody's benefit)
N++, N+-, N-+, N-- are the counts for (hel=+,tgt=+), (hel=+,tgt=-),
(hel=-,tgt=+) (hel=-,tgt=-)
Recall the stuff from jason, we form 4 asymmetries per sector:
A1 = N++ - N+- / N++ + N+-
A2 = N-+ - N-- / N-+ + N--
A3 = N++ - N-+ / N++ + N-+
A4 = N+- - N-- / N+- + N--
However our results were so and so and our statistics made it difficult
to give an answer. So we define an average asymmetry as
A_ave = (N++ + N--) - (N+- + N-+) / (N++ + N--) + (N+- + N-+)
To form this asymmetry just add the counts, and accounts later for the
relative normalization given by (q++ + q--)/(q+- + q-+) (that was wrong
last night, but it was a little effect). This is because you've now made
the ansatz N++ = N-- ; N+- = N-+ so the relative normalization is clearly
given by the sum of the charges.
The other virtue of A_ave is that you are now left with one asymmetry per
sector. We can now fit a dilution factor (= P_beam * P_target) to both
sector simultaneously because our data is given by Pe*Pt*Delta, and
we know how to parametrize Delta for L/R sectors (of course, it is the
theory asymmetry, depends only on kinematics). So out fir searches for
the scale factor.
I'll figure out how to do root fits myself but basically the result is
"very small" (yesterday's plot just scaled the asymmetry). You could in
principle fit also over the 2 x 4 direct asymmetries but then you don't
really have independent data points so I don't know where we end up with
the dilution factor (*remember* the whole idea is to use this reaction to
*measure* P_e * P_t).
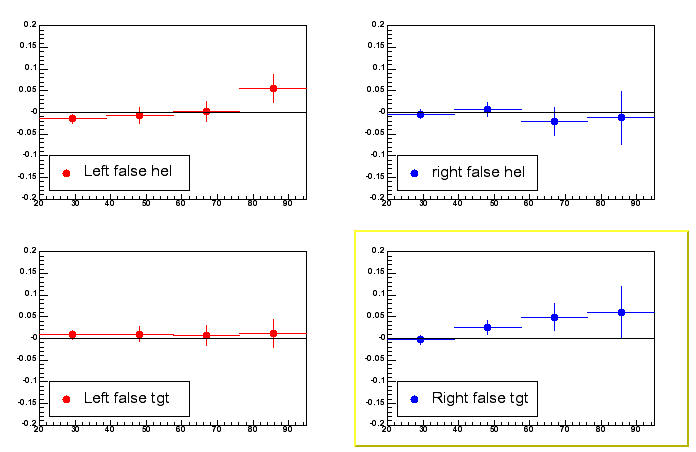
Now I also added false asymmetries: at least initially they are
defined as
false_hel = Asym[ (N++ + (q++/q+-)*N+-) , (N-+ + (q-+/q--)*N--) ]
where the two "pure" beam helicity states have an internal normalization
(hence (N++ + (q++/q+-)*N+-) and (N-+ + (q-+/q--)*N--) ), and then also a
relative normalization (q++/q-+) to account for charge normalization in
the asymmetry. Finally:
false_target = Asym[ (N++ + (q++/q-+)*N-+) , (N+- + (q+-/q--)*N--) ]
True the most direct way to check for false asymmetries is with unpol
data, but the above in an overally check. Even in the most diabolic
scenarios (put all false asymmetries were it suits you best) we don't get
an overall asymmetry much higher than 5%.
-- tancredi
________________________________________________________________________________
Tancredi Botto, phone: +1-617-253-9204 mobile: +1-978-490-4124
research scientist MIT/Bates, 21 Manning Av Middleton MA, 01949
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
This archive was generated by hypermail 2.1.2 : Mon Feb 24 2014 - 14:07:29 EST