Hi,
On the subject of Monte Carlo errors, DGen uses a quasi-random (Sobol
generator) instead of the standard pseudo-random generators. (Chi,
correct me if I'm wrong). According to NR, these sequences are not
random at all, but are designed to uniformly cover the domain "maximally
avoiding each other". The result is that the errors go not as sqrt(m),
but as log(m) or so. If you use the Jason's GetAsymmetry ROOT function
to calculate these asymmetries, make sure that you update to v4-03-02
because this is the first version that correctly calculates the
asymmetry errors using non-Poisson statistics.
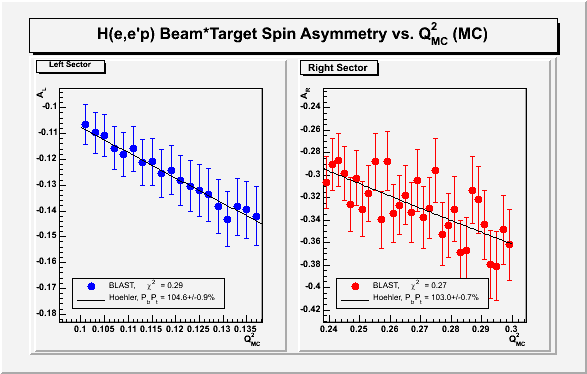
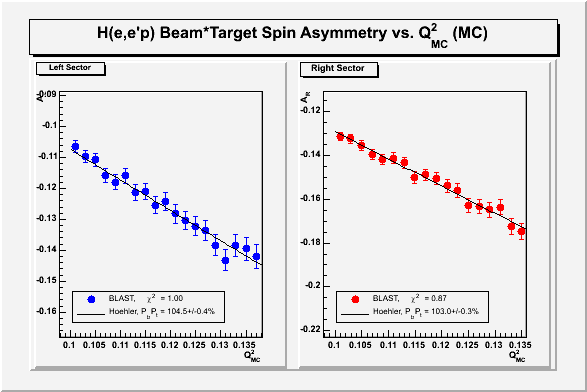
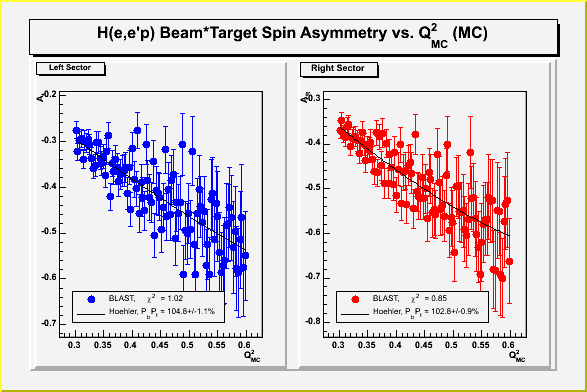
The attached plots illustrate this. The first one was done using
poisson statistics. The second plots were done with \alpha*log(m)
errors, where \alpha=2.5 was chosen so that chi^2=1 for the fit. Now
the chi^2 is the same for both low Q^2 and high Q^2.
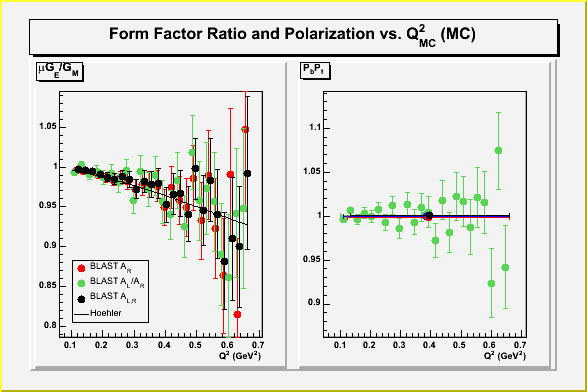
The last plot shows the corrected form factor ratio extraction from
Monte Carlo. The results I showed at the Wed. analysis meeting had the
wrong error bars, and were also shifted up by 2% because of some mistake
which made DGen using the default 45 degree holding field instead of the
map.
--Chris
Douglas Hasell wrote:
> Hi,
>
> Just a follow up on the uncertainties in Monte Carlo calculations
> which I raised a couple of weeks ago.
>
> It's rather obvious actually. Generating Monte Carlo events based
> on a uniform random number distributed between 0 and 1 is a binomial
> distribution. So if you generate "n" events and "m" find their way
> into a given bin then the probability for an event going into that bin
> is "p=m/n". If you repeat the Monte Carlo calculation many times then
> the mean number of events which go to that bin is "np" and the
> variance from calculation to calculation is "np(1-p)" where "p" now is
> the average value of "m/n" for all the MC calculations. Since the
> uncertainty (standard deviation, RMS) is the square root of the
> variance (assuming the sample is statistically significant); then the
> uncertainty in that bin is "sqrt(np(1-p))" or
> sqrt(m(1-m/n))". This approaches gaussian or normal distribution when
> "m/n~0" at which point the uncertainty in the number of events in the
> bin is the square root of the number of entries in that bin.
>
> So the conclusion is: if you generate a large number of MC events
> and only a small fraction of them end up in a given bin ( ie "m/n~0" )
> you can use the square root of the number of entries in that bin (
> "sqrt(m)" ) for the uncertainty. Otherwise you must use "sqrt( m
> (1-m/n) )".
>
> Hope that is clear. Let me know if there are any problems with
> this.
>
>
> Cheers,
>
> Douglas
>
> 26-415
> M.I.T. Tel:
> +1 (617) 258-7199
> 77 Massachusetts Avenue Fax: +1 (617)
> 258-5440
> Cambridge, MA 02139, USA E-mail:
> hasell@mit.edu
This archive was generated by hypermail 2.1.2 : Mon Feb 24 2014 - 14:07:32 EST